Modelling and Prediction of Photovoltaic Power Output Using Artificial Neural Networks

The sun is one of the primary sources of energy for most of the natural processes such as heat, wind, and rain.

Let us try to predict how much solar power will our plant produce?

The most effective conversion of sunlight into chemical energy can be seen in photosynthesis. Currently, humankind is using fossil fuels as their primary energy source. Still, fossil fuels are not an appropriate source of energy. This leads to using sunlight as a renewable energy source to produce electricity, called solar power. Moreover, solar energy is green energy, and it is environmentally friendly. Photovoltaic panels and solar thermal are the primary sources of electricity from solar energy. The prediction of power generation from solar energy is gaining considerable attention due to the increment of power generation from solar energy. Numerical models have been developed to forecast weather and solar power; however, they require a powerful computing system.

An artificial neural network assimilates the human brain learning system. As a result, it can find an input-output relationship for linear and nonlinear systems with less computational effort. This leads to the extensive usage of artificial neural networks to forecast various criteria, such as irradiance and temperature. In general, neural networks are universal approximators.

The power generation of photovoltaic panels depends on solar radiation, temperature, humidity, and so on. These parameters are naturally variable and non-schedulable; thus, the amount of generated power is generally unknown. Previous researchers have affirmed feedforward backpropagation (FFBP) and the general regression neural network (GRNN) as effective modeling and prediction methods. On the other hand, power planning is necessary for the cost efficiency of power generation, for which power forecasting is essential.

The application of ANN has some advantages, such as the flexible mapping function in a neural network. In addition, the neural network can generalize from a limited set of data points and give good results at new data points. However, only a few describe forecasting models used to predict the daily energy production of the PV plant directly.

Feedforward Back Propagation (FFBP)

Among the different forms of ANN, feedforward backpropagation and general regression neural networks are proposed in this research. A feedforward neural network is defined as a simple type of neural network in which the information flow is in the forward direction. The structure of the FFNN is in three different layers. An input layer is used for data collection, a hidden layer for data processing by neurons, and an output layer for the results. Backpropagation (BP) is assumed as a popular learning technique for feedforward neural networks. Therefore the FFBP is defined as a model for forecasting parameters and the prediction diagram using FFBP.

The FFNN is defined as an MLP network with particular input values. These values, multiplied by their weight, are led to the hidden layer by neurons. He provided a feedforward multilayer perception model with four inputs for the calculation. The training process for the backpropagation algorithm includes a few steps. First, the weights are initialized for the neurons, and the measured output is compared with the desired value to calculate the error. In the second step, the weights are changed based on the error. In this way, the error is propagated backward to update the weights of the previous layers.

Methodology

Meteorological data such as the temperature and solar irradiance were collected from the Indian Meteorological Department (IMD), including the daily minimum, maximum temperature, and solar irradiance starting from January 1, 2016, to December 31, 2016. In addition, all data was collected from the solar plants under the purview of SolarAMC. One of their sites in India was taken as a sample for the model.

The feedforward back propagation method is used as the neural network model for this project. The applied flowchart of FFBP is shown in the figure below:

As shown in the figure above, the prediction results are based on reading the testing and training data and using FFBP. Before the training process, all the data must be normalized. Various normalization methods are used for neural networks to increase the reliability of the trained network. The Min-Max normalization is applied in this project as follows:

where a is the normalized value and b is a non-normalized value. For this project a_max = 1 and a_min =-1.

After obtaining the result, the normalized values become normal by using the following formula:

The mean squared error (MSE) is used for evaluation of predictive power as follows:

Where overline(Z_t )  is a vector of the N prediction and Z_t is the vector of the real values.

Results and Implications

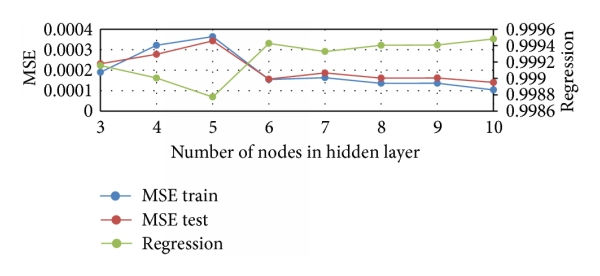
A trial to investigate the number of nodes in the hidden layer is evaluated to find the MSE of the FFBP neural network. The data table below represents the training MSE, testing MSE, and regression value for different numbers of hidden nodes for FFBP. In addition, a line chart shows a graphical visualization of MSE and regression based on the number of nodes in the hidden layer.

The comparison between the simulated results of the FFBP and the real data for the solar panel's power in 2016 is provided in the following figures. These figures illustrate these comparisons for January, February, and March 2016.

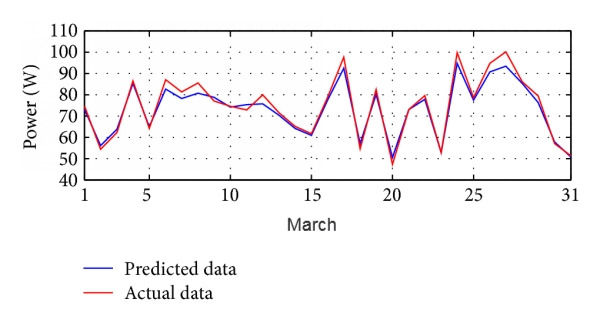
The results for these three months demonstrate that the results are accurate for the FFBP model. The hidden neurons and the number of epochs in this calculation are 10 and 1000, respectively. The same comparison for one year (2016) is provided in the below figure with six hidden neurons and 1000 epochs.

The above figure shows that the differences between predicted and real power are shallow, and a high accuracy level of accuracy is achieved by using FFBP. Although the number of hidden layers is increased from 6 hidden neurons to 10 hidden neurons, the level of accuracy is very close. The following figure presents the regression of the calculated and actual data. As shown in this figure, the measured error is very low.

Conclusion

Power prediction for photovoltaic panels is needed for accurate power planning. In this project, the generated power of a solar panel has been estimated using mathematical equations. Afterward, the meteorological data and estimated power were used for training the FFBP model. This neural network has shown good modeling performance.

Softwares/Libraries used

Python

Excel